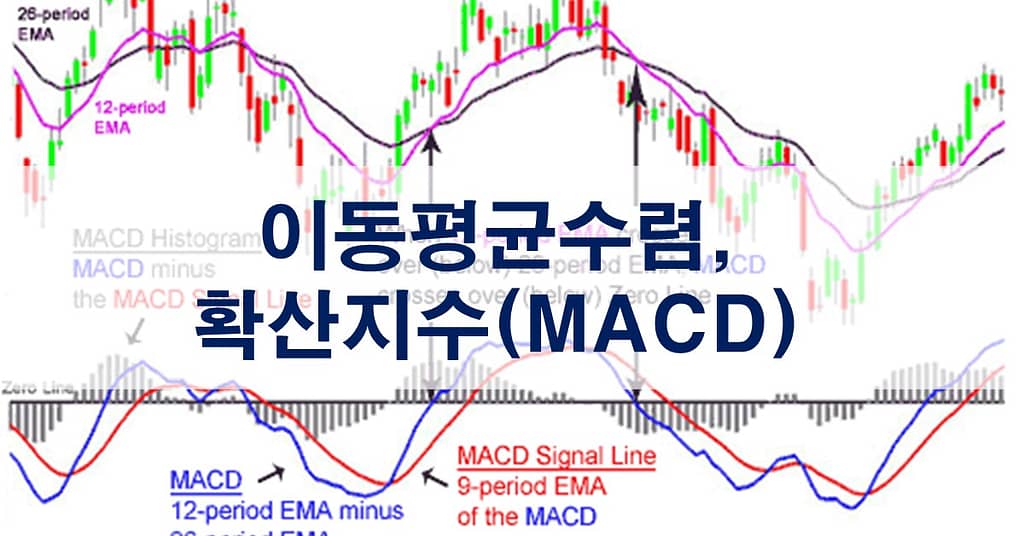
이동평균(moving average, MA)은 가격 변화의 추세를 분석하기 위해 전체 데이터 집합을 여러 하위 집합으로 나누어 평균을 계산하는 기법입니다.
이동평균(moving average, MA)
이동평균(moving average, MA)은 가격 변화의 추세를 분석하기 위해 전체 데이터 집합을 여러 하위 집합으로 나누어 평균을 계산하는 기법입니다. 이동평균을 계산하면서 구한 평균 값을 날짜별로 점으로 찍고 이를 선으로 연결하면 이동평균선을 얻을 수 있습니다.
이동평균의 종류
이동평균에는 단순이동평균(simple moving average), 누적이동평균(cumulative moving average), 가중이동평균(weighted moving average), 지수이동평균(exponential moving average) 등 여러 종류가 있습니다.
단순이동평균은 이미 이전에 설명한 대로 계산되며, 누적이동평균은 특정 구간을 정하지 않고 현재까지의 모든 데이터에 대한 평균을 계산하는 방식입니다.
가중이동평균은 최근 데이터에 더 높은 가중치를 부여하여 평균을 계산하는 방법입니다.
지수이동평균은 가중치를 사용하면서도 오래된 데이터에 점차 감소하는 가중치를 적용하여 평균을 계산합니다.
이동평균의 활용
이동평균의 장점은 구간별 평균을 계산하므로 특정 일자의 가격 변동이 평균에 미치는 영향을 파악할 수 있고, 구간이 지속적으로 이동하기 때문에 과거 데이터의 영향력을 점차 감소시키고 최신 데이터를 반영할 수 있다는 점입니다. 또한, 다양한 구간을 사용하여 구간별 특징을 비교할 수도 있습니다.
그러나 이동평균 구간이 너무 길면 짧은 구간의 신호를 파악하지 못하고, 너무 짧으면 가격 변동 추이를 제대로 관찰할 수 없는 문제가 발생할 수 있습니다. 따라서 구간을 어떻게 설정하느냐는 이동평균을 제대로 활용하기 위한 중요한 결정 요소입니다. 또한, 이동평균은 많은 과거 데이터와 적은 현재 데이터로 평균을 계산하므로 최신 데이터를 늦게 반영하는 단점이 있습니다.
바이낸스 거래소에서의 이동평균
바이낸스 차트에서 제공하는 지수이동평균(EMA)은 일반적으로 단기 7, 중기 25, 장기 99로 설정됩니다. 이는 분 단위로 각각 7분, 25분, 99분 동안의 지수이동평균을 계산하여 그래프에 표시한 것입니다.
일반적으로 이동평균선은 장기, 중기, 단기 이동평균을 함께 화면에 표시하며, 각 이동평균선이 교차하는 지점을 추세 전환점으로 판단하는 경우가 많습니다.
가상화폐 선물거래는 초보자에게도 접근하기 쉽고 안정적인 수익을 얻을 수 있는 투자 방법입니다.
선물거래의 기본 개념과 장점, 주의사항을 충분히 이해한 뒤에 투자를 시작하는 것이 중요합니다. 지식과 경험을 쌓아가며 리스크를 효과적으로 관리하고, 신뢰할 수 있는 거래소에서 안전하고 효과적인 가상화폐 선물거래를 진행해 보세요.